8.1. Basic Tutorials
The key modelling concepts in DAE Tools:
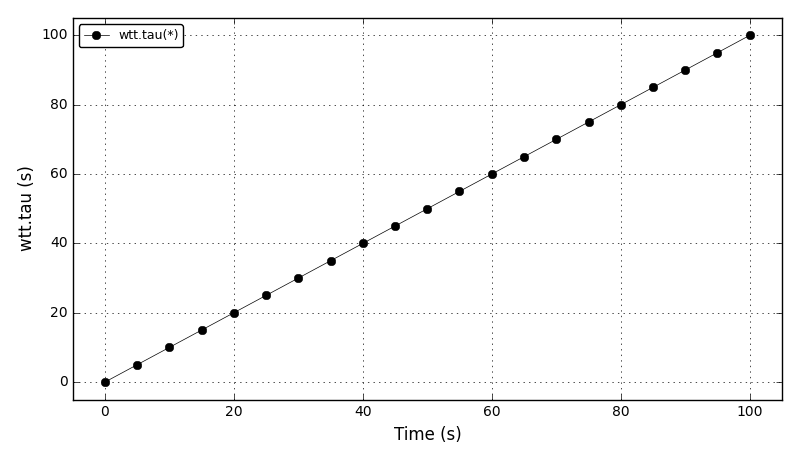
| What’s the time? (AKA: Hello world!) |
Importing DAE Tools pyDAE module(s), units and variable types
developing models, setting up a simulation, declaring auxiliary
objects (DAE solver, data reporter, log), simulation run-time
options, running a smulation. |
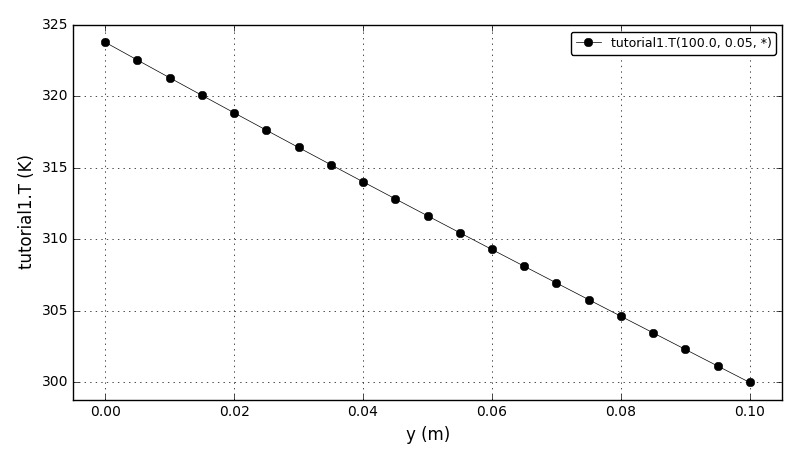
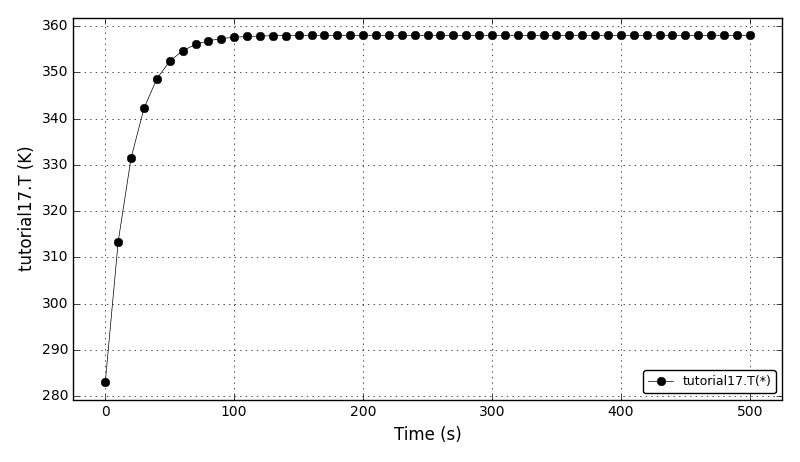
| Tutorial 1 |
Using distribution domains, distributing parameters/variables/equations on domains,
using derivative functions (dt, d, d2), setting boundary and initial conditions. |
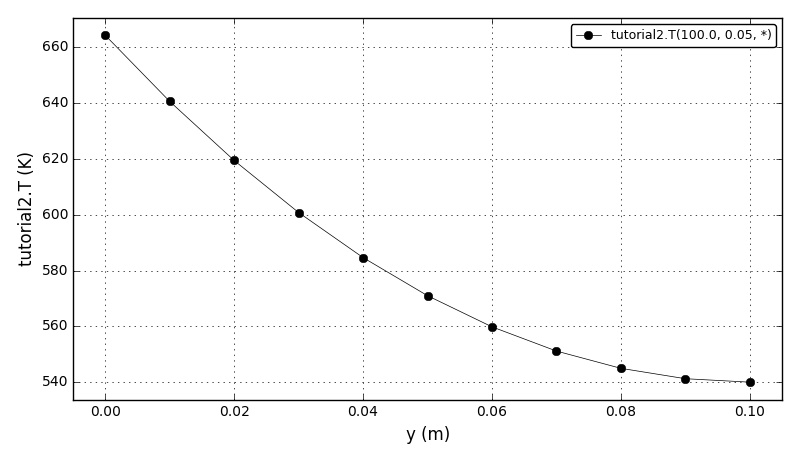
| Tutorial 2 |
Using arrays (discrete distribution domains), specifying degrees of freedom, setting initial guesses. |
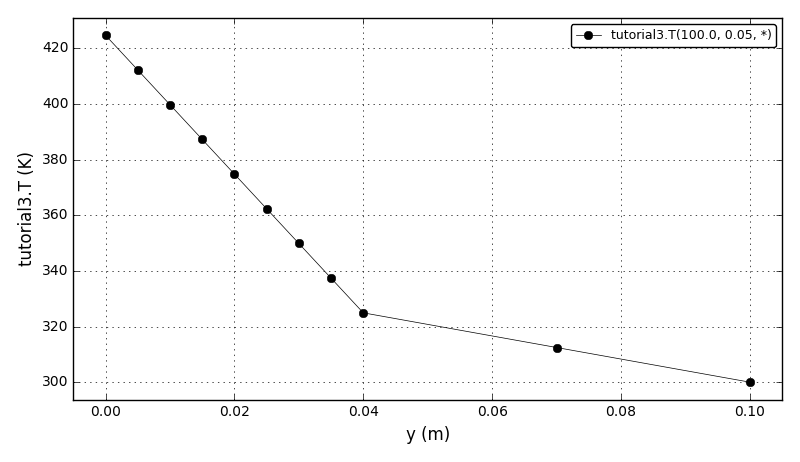
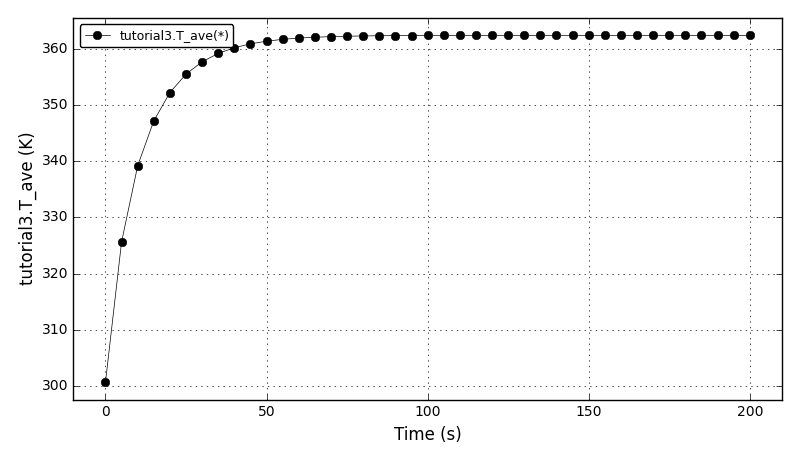
| Tutorial 3 |
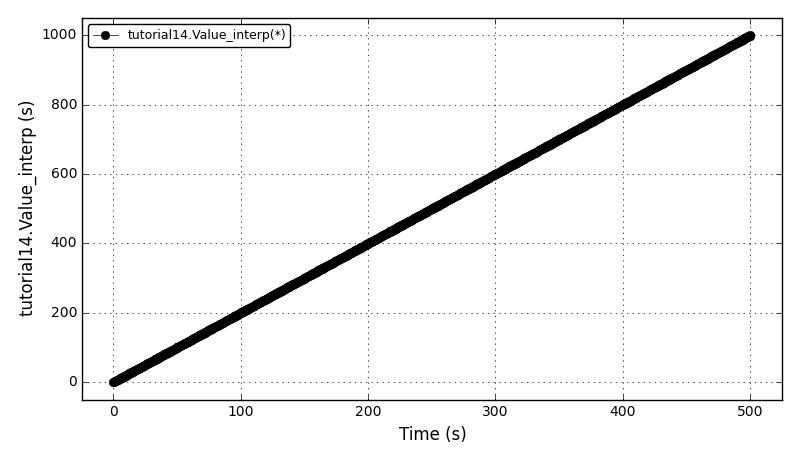
Declaring arrays of variable values (Array function) and using functions that operate on them arrays,
using the Constant function, making non-uniform grids. |
| Tutorial 6 |
Using ports, making port connections, declaring components (instances of other models). |
| Tutorial 10 |
Saving and restoring initialisation files, evaluating integrals. |
Support for discrete systems:
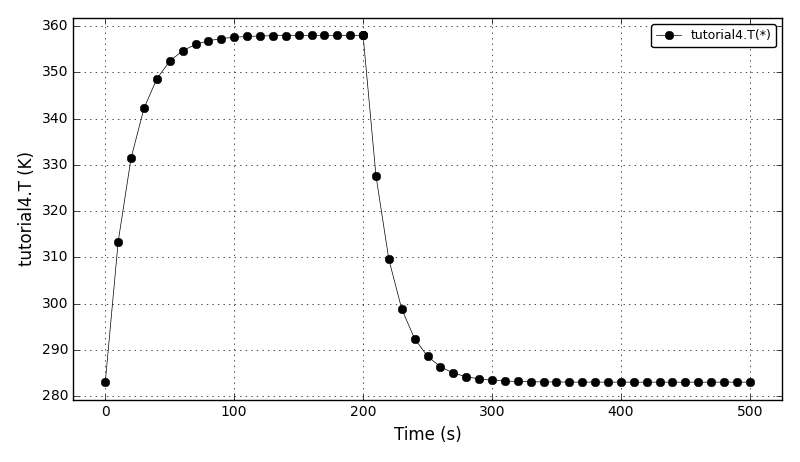
| Tutorial 4 |
Declaring discontinuous equations (symmetrical state transition networks: daeIF statements). |
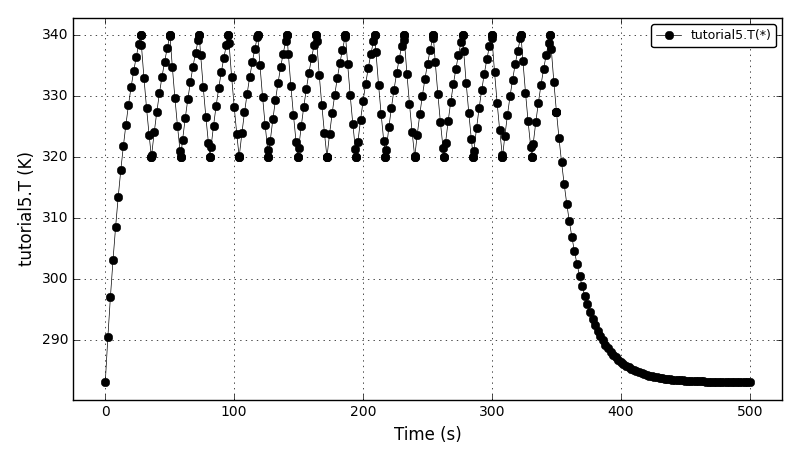
| Tutorial 5 |
Declaring discontinuous equations (non-symmetrical state transition networks: daeSTN statements). |
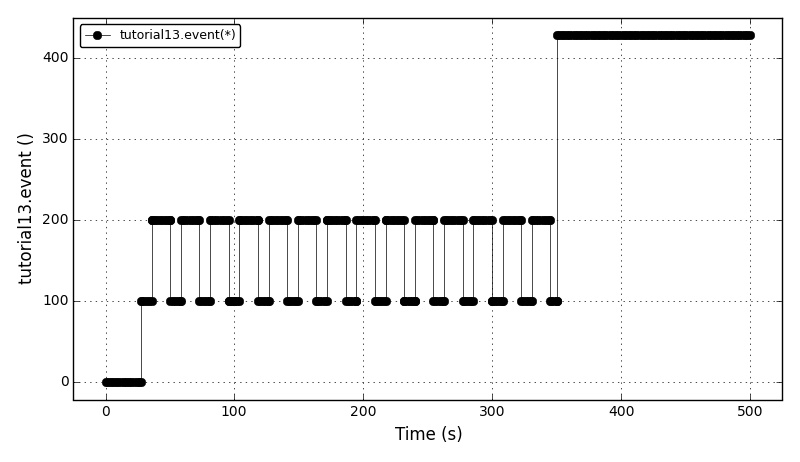
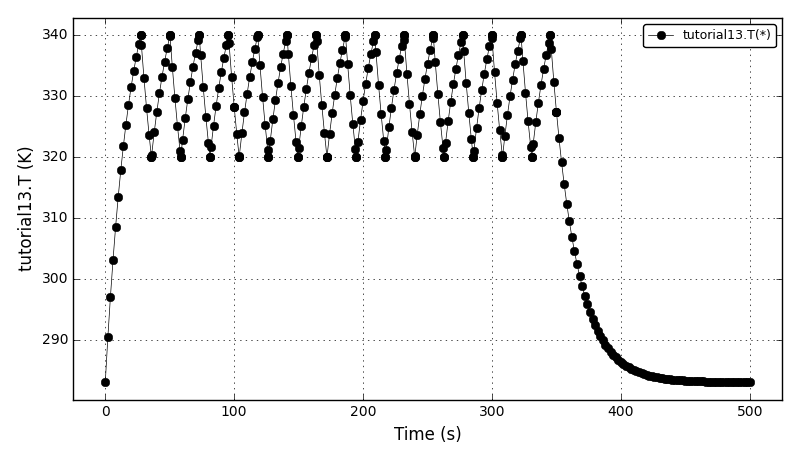
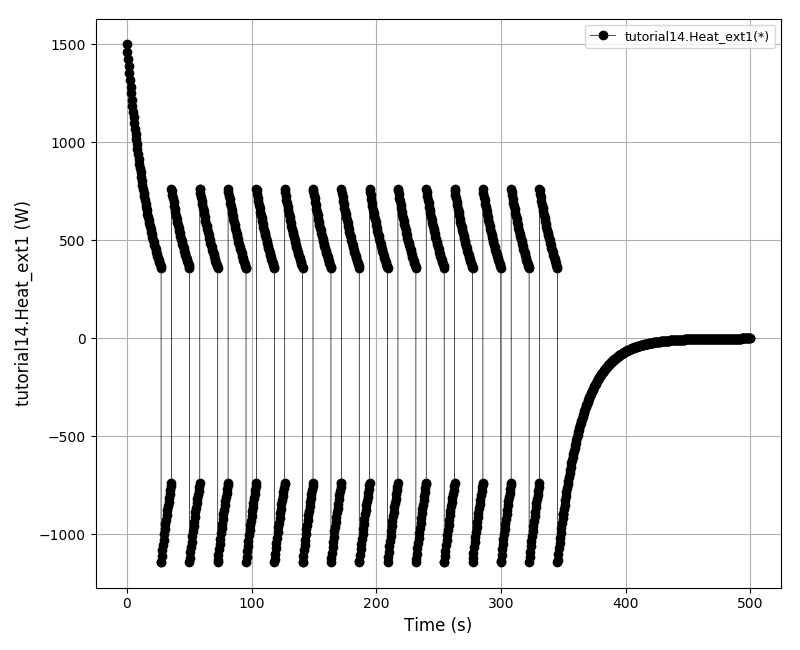
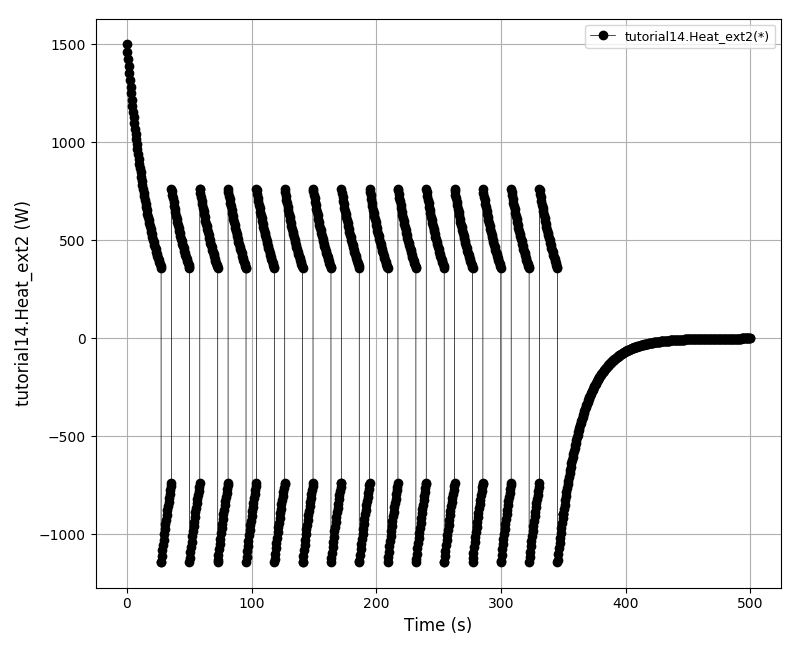
| Tutorial 13 |
Using event ports, handling events using ON_CONDITION() and ON_EVENT() functions,
and declaring user defined actions. |
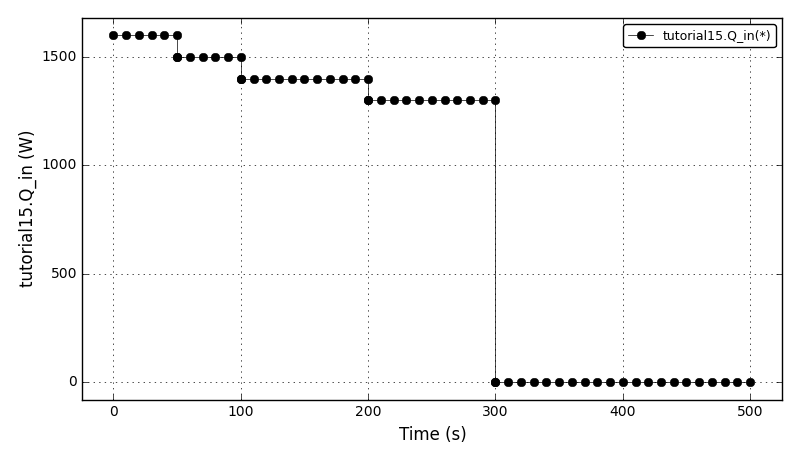
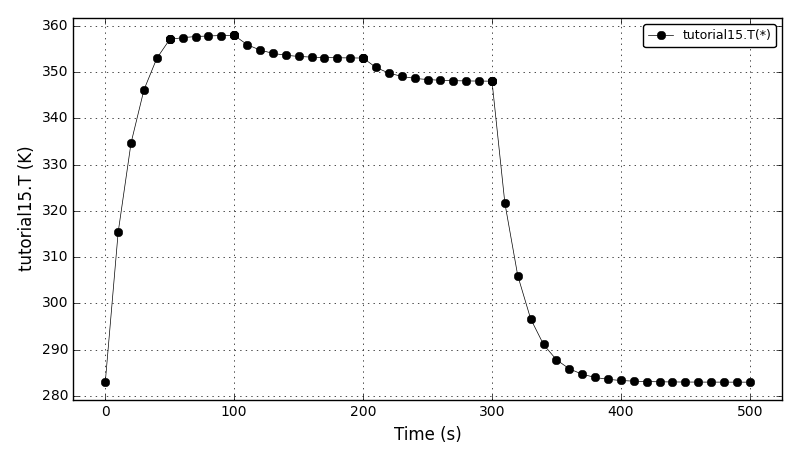
| Tutorial 15 |
Declaring nested state transitions. |
The simulation options:
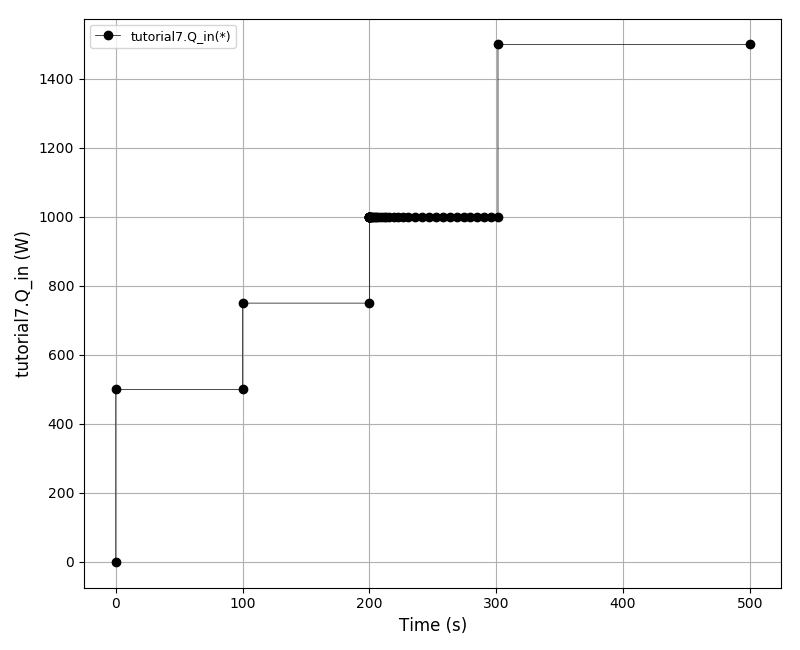
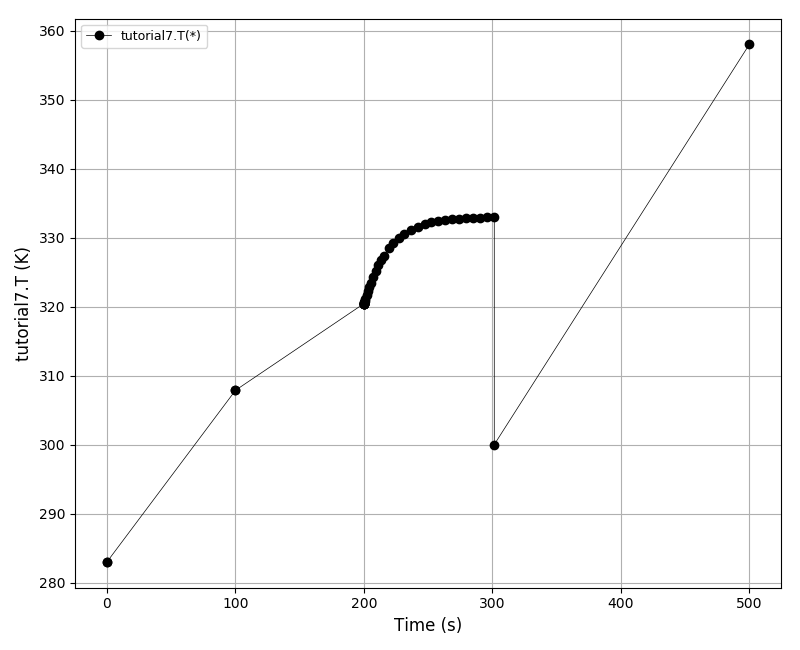
| Tutorial 7 |
Making user-defined schedules (operating procedures), resetting the values of degrees of freedom and
resetting initial conditions. |
Data reporting:
| Tutorial 8 |
Using data reporters to write the results into files (Matlab, MS Excel, JSON, XML, HDF5, VTK, Pandas),
developing custom data reporters. |
DAE and LA solvers:
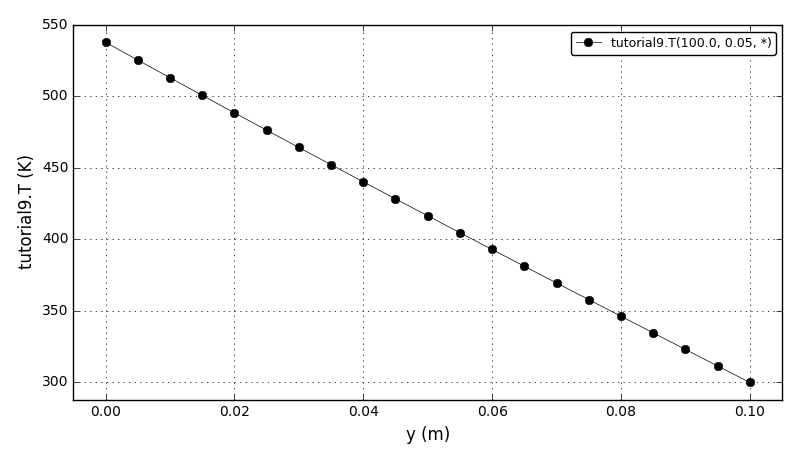
| Tutorial 9 |
Using available linear equations solvers (SuperLU, SuperLU_MT, Trilinos Amesos, IntelPardiso, Pardiso). |
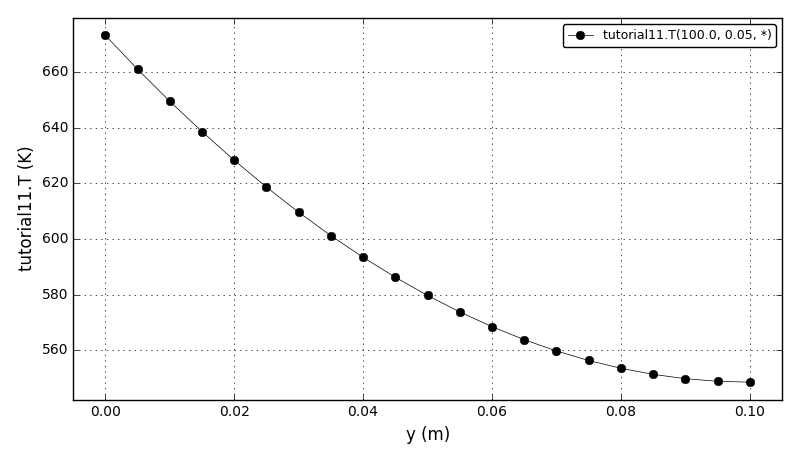
| Tutorial 11 |
Using iterative linear equations solvers (Trilinos AztecOO) and preconditioners
(built-in AztecOO, Ifpack, ML). |
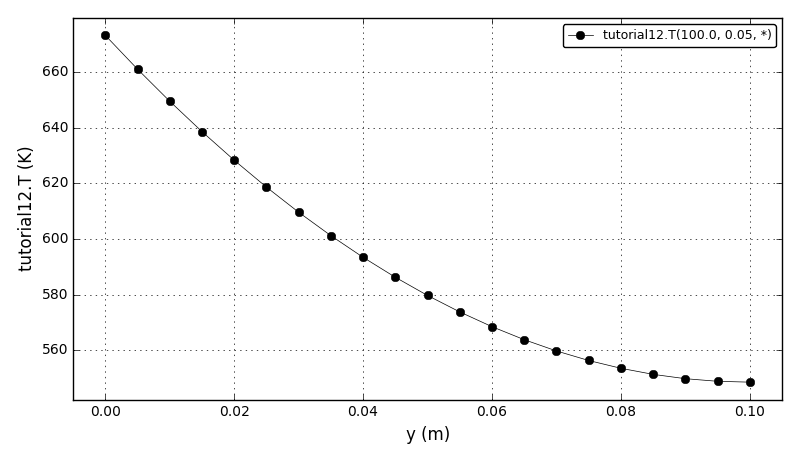
| Tutorial 12 |
Using SuperLU and SuperLU_MT solvers and their options. |
External functions:
Logging:
Interoperability with NumPy:
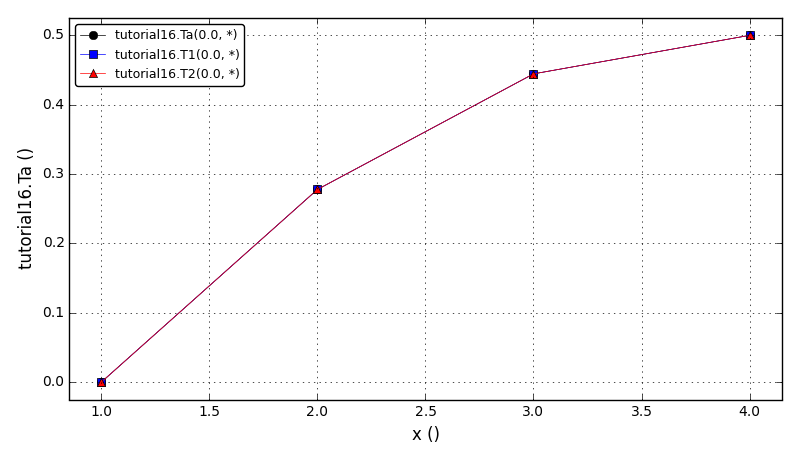
| Tutorial 16 |
Using DAE Tools variables and NumPy functions to solve a simple stationary 1D heat conduction
by manually assembling Finite Element stiffness matrix and load vector. |
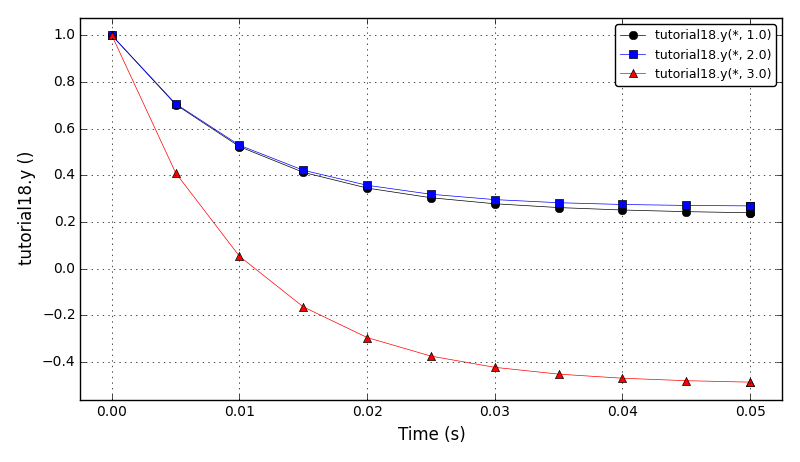
| Tutorial 18 |
Using DAE Tools variables and NumPy functions to generate and solve a simple ODE system. |
Thermophysical property packages:
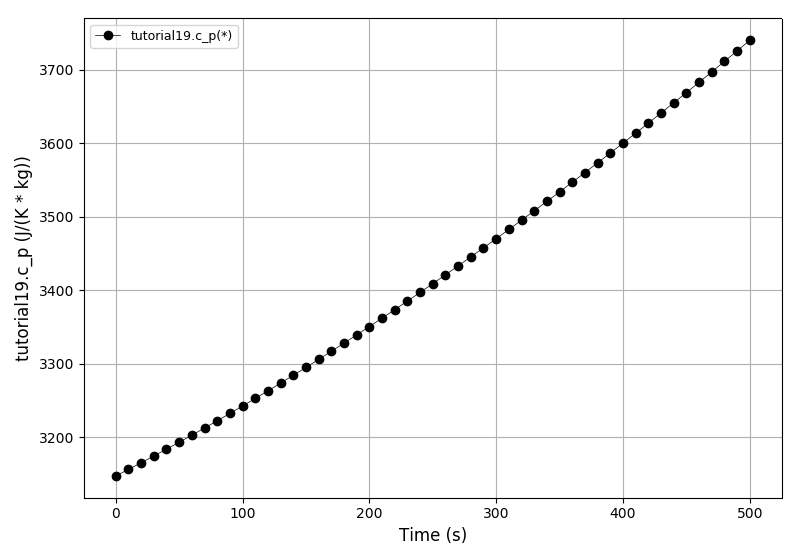
| Tutorial 19 |
Using thermophysical property packages in DAE Tools. |
Variable constraints:
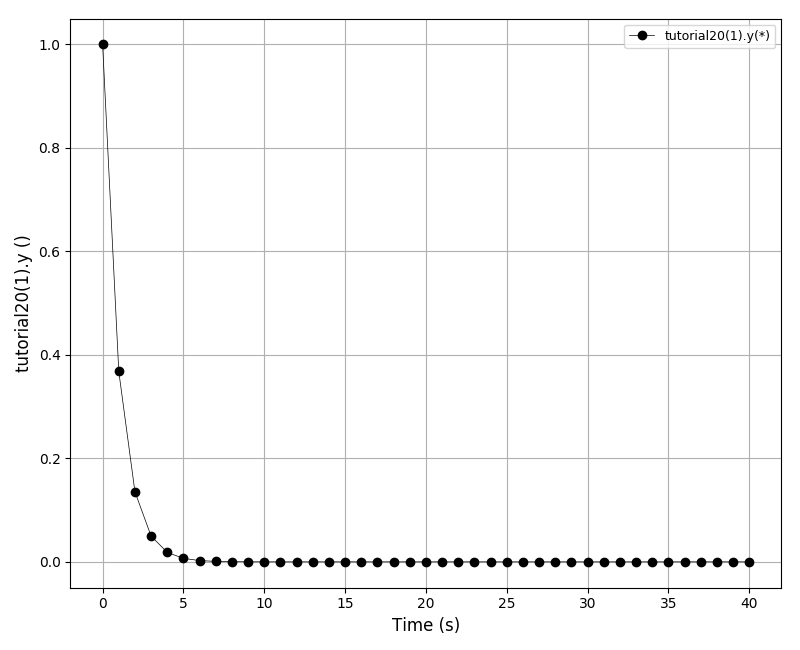
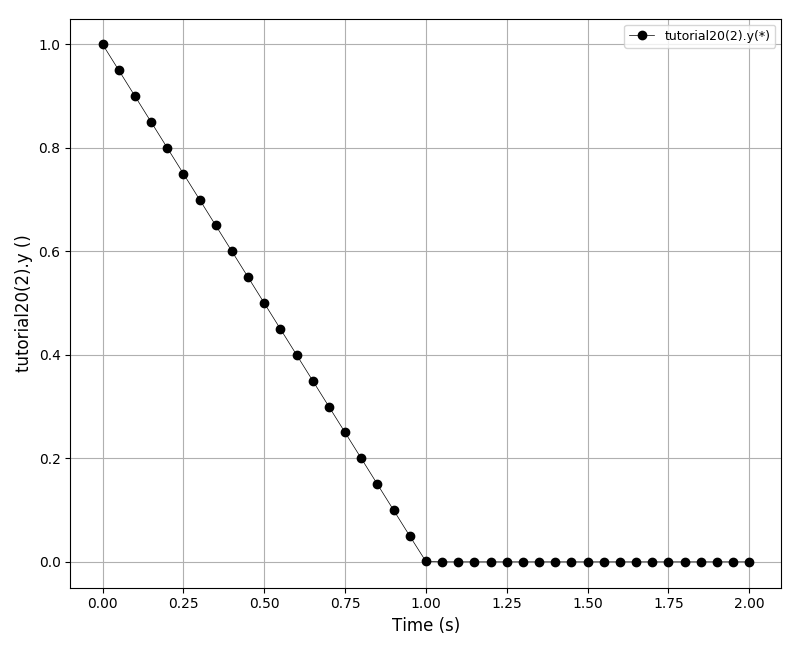
| Tutorial 20 |
Specifying variable constraints in DAE Tools. |
Equation evaluation modes:
| Tutorial 21 |
Specifying different equation evaluation modes and evaluators. |
 DAE Tools
1.9.0
DAE Tools
1.9.0