8.6. Sensitivity Analysis Examples¶

8.6.1. Sensitivity Analysis Example 1¶

This tutorial illustrates calculation of the sensitivity of the results with respect to the model parameters using forward sensitivity analysis method in DAE Tools.

This model has one state variable (T) and one degree of freedom (Qin). Qin is set as a parameter for sensitivity analysis.

The integration of sensitivities per specified parameters is enabled and the sensitivities can be reported to the data reporter like any ordinary variable by setting the boolean property simulation.ReportSensitivities to True.

Raw sensitivity matrices can be saved into a specified directory using the simulation.SensitivityDataDirectory property (before a call to Initialize). The sensitivity matrics are saved in .mmx coordinate format where the first dimensions is Nparameters and second Nvariables: S[Np, Nvars].

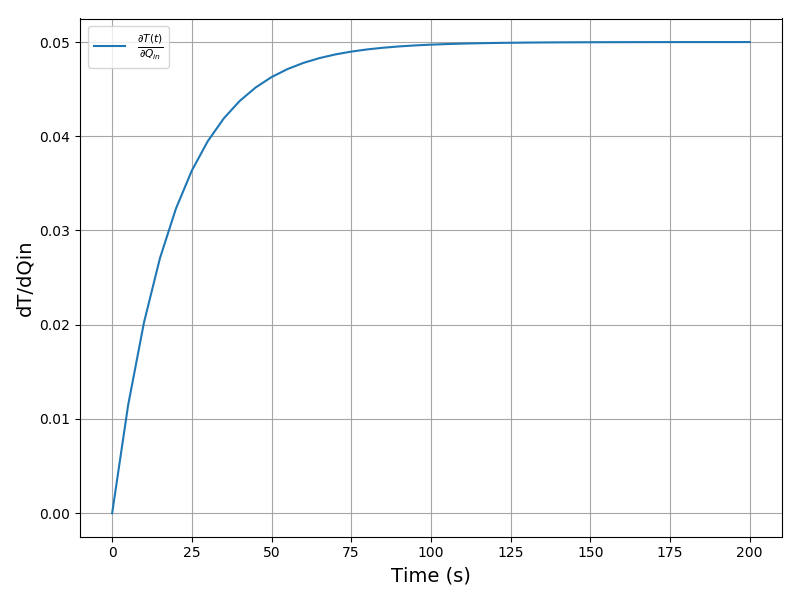
The plot of the sensitivity of T per Qin:

Files

8.6.2. Sensitivity Analysis Example 2¶

This tutorial illustrates the local derivative-based sensitivity analysis method available in DAE Tools.

The problem is adopted from the section 2.1 of the following article:

• A. Saltelli, M. Ratto, S. Tarantola, F. Campolongo. Sensitivity Analysis for Chemical Models. Chem. Rev. (2005), 105(7):2811-2828. doi:10.1021/cr040659d

The model is very simple and describes a simple reversible chemical reaction A <-> B, with reaction rates k1 and k_1 for the direct and inverse reactions, respectively. The reaction rates are uncertain and are described by continuous random variables with known probability density functions. The standard deviation is 0.3 for k1 and 1 for k_1. The standard deviation of the concentration of the species A is approximated using the following expression defined in the article:

stddev(Ca)**2 = stddev(k1)**2 * (dCa/dk1)**2 + stddev(k_1)**2 * (dCa/dk_1)**2

The following derivative-based measures are used in the article:

• Derivatives dCa/dk1 and dCa/dk_1 calculated using the forward sensitivity method

• Sigma normalised derivatives:

  S(k1)  = stddev(k1) / stddev(Ca) * dCa/dk1
  S(k_1) = stddev(k_1)/ stddev(Ca) * dCa/dk_1
  

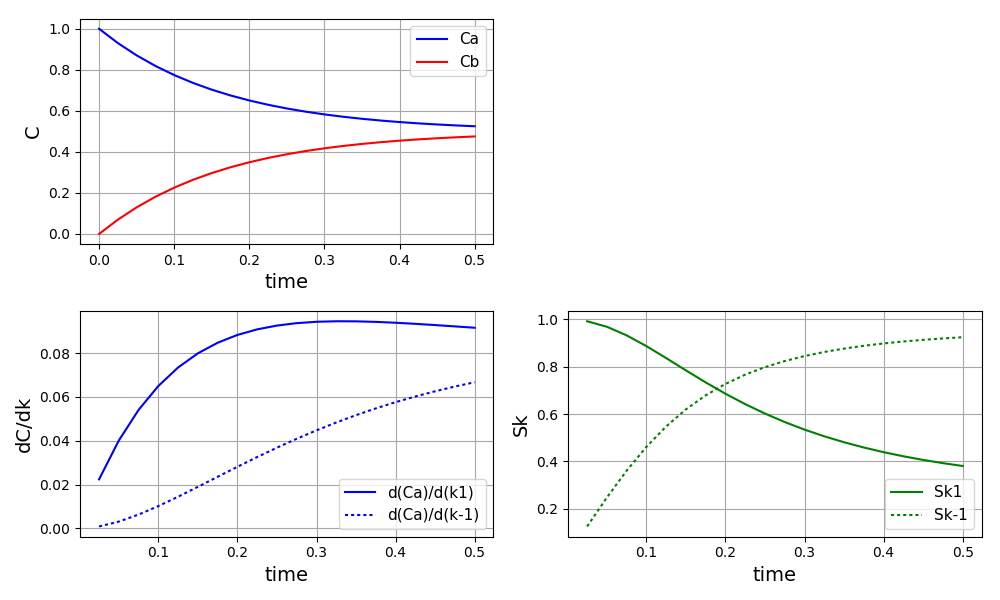
The plot of the concentrations, derivatives and sigma normalised derivatives:

Files

8.6.3. Sensitivity Analysis Example 3¶

This tutorial illustrates the global variance-based sensitivity analysis methods available in the SALib python library.

The problem is adopted from the section 2.6 of the following article:

• A. Saltelli, M. Ratto, S. Tarantola, F. Campolongo. Sensitivity Analysis for Chemical Models. Chem. Rev. (2005), 105(7):2811-2828. doi:10.1021/cr040659d

The model describes a thermal analysis of a batch reactor, with exothermic reaction A -> B. The model equations are written in dimensionless form.

Three global sensitivity analysis methods available in SALib are applied:

• Morris (Elementary Effect/Screening method)
• Sobol (Variance-based methods)
• FAST (Variance-based methods)

Results from the sensitivity analysis:

-------------------------------------------------------
       Morris (N = 510)
-------------------------------------------------------
    Param          mu        mu*   mu*_conf      Sigma
        B    0.367412   0.367412   0.114161   0.546276
    gamma   -0.040556   0.056616   0.021330   0.111878
      psi    0.311563   0.311563   0.103515   0.504398
  theta_a    0.326932   0.326932   0.102303   0.490423
  theta_0    0.021208   0.023524   0.016015   0.074062
-------------------------------------------------------

-------------------------------------------------------
       Sobol (N = 6144)
-------------------------------------------------------
    Param          S1    S1_conf         ST    ST_conf
        B    0.094110   0.078918   0.581930   0.154737
    gamma   -0.002416   0.012178   0.044354   0.027352
      psi    0.171043   0.087782   0.524579   0.142115
  theta_a    0.072535   0.042848   0.523394   0.165736
  theta_0    0.002340   0.004848   0.008173   0.005956

Parameter pairs          S2    S2_conf
        B/gamma    0.180427   0.160979
          B/psi    0.260689   0.171367
      B/theta_a    0.143261   0.154060
      B/theta_0    0.177129   0.156582
      gamma/psi    0.000981   0.027443
  gamma/theta_a    0.004956   0.036554
  gamma/theta_0   -0.009392   0.027390
    psi/theta_a    0.166155   0.172727
    psi/theta_0   -0.016434   0.129177
theta_a/theta_0    0.109057   0.127287
-------------------------------------------------------

---------------------------------
       FAST (N = 6150)
---------------------------------
    Param          S1         ST
        B    0.135984   0.559389
    gamma    0.000429   0.029026
      psi    0.171291   0.602461
  theta_a    0.144617   0.534116
  theta_0    0.000248   0.040741
---------------------------------

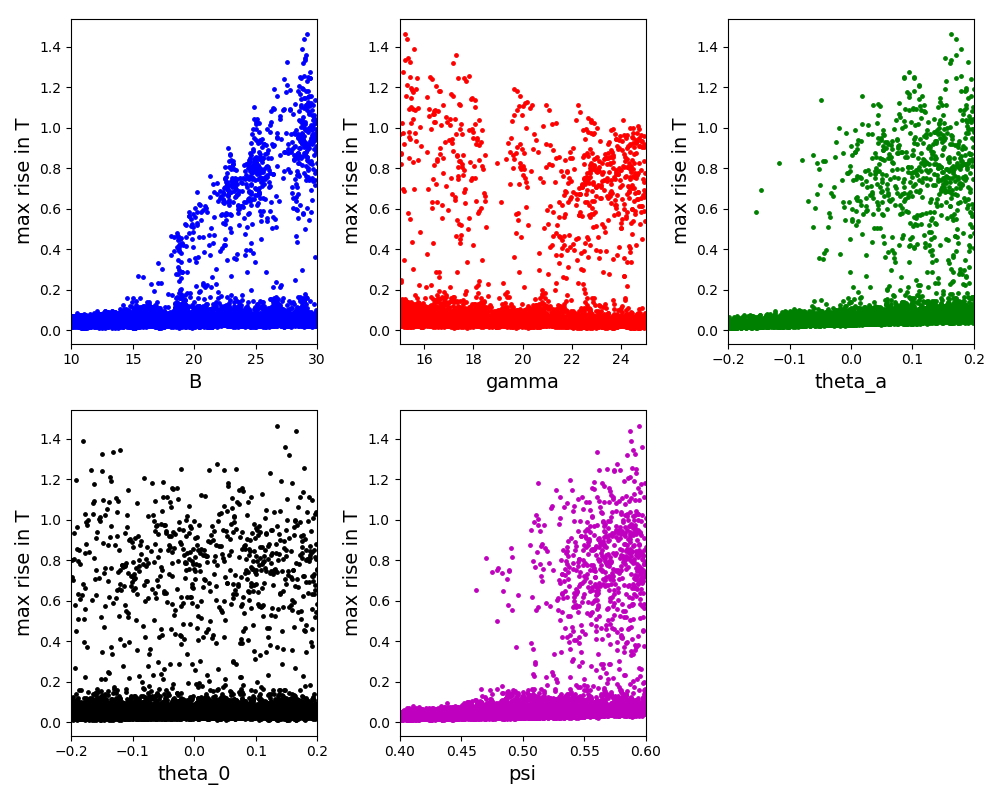
The scatter plot for the Morris method:

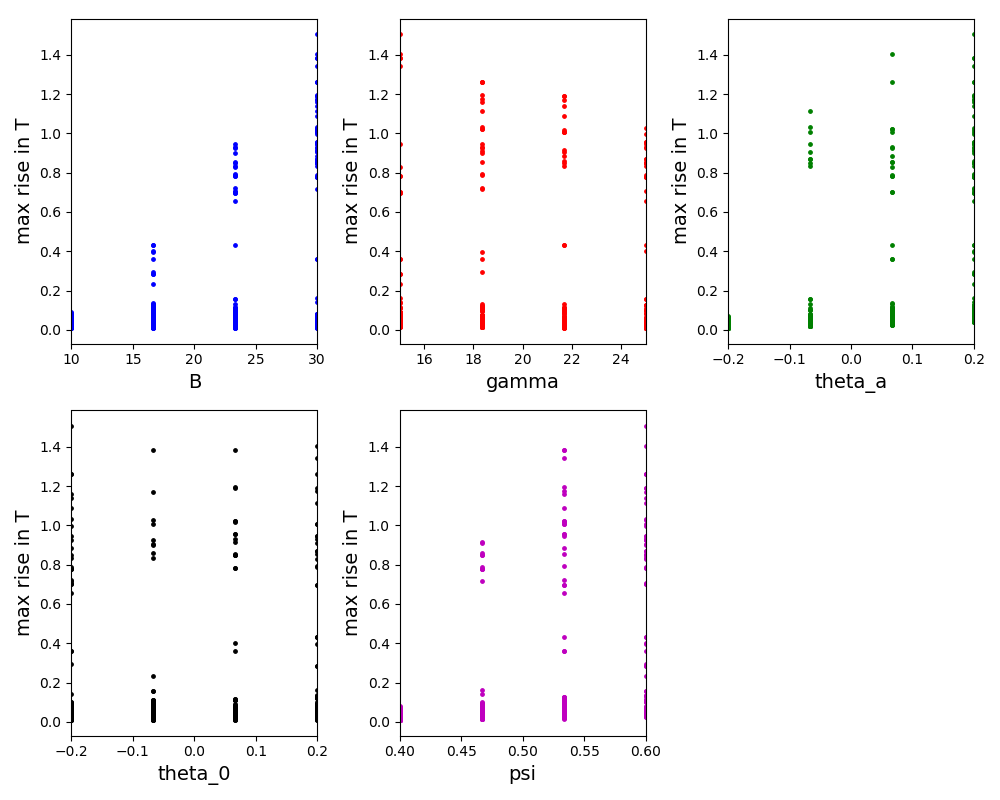
The scatter plot for the Sobol method:

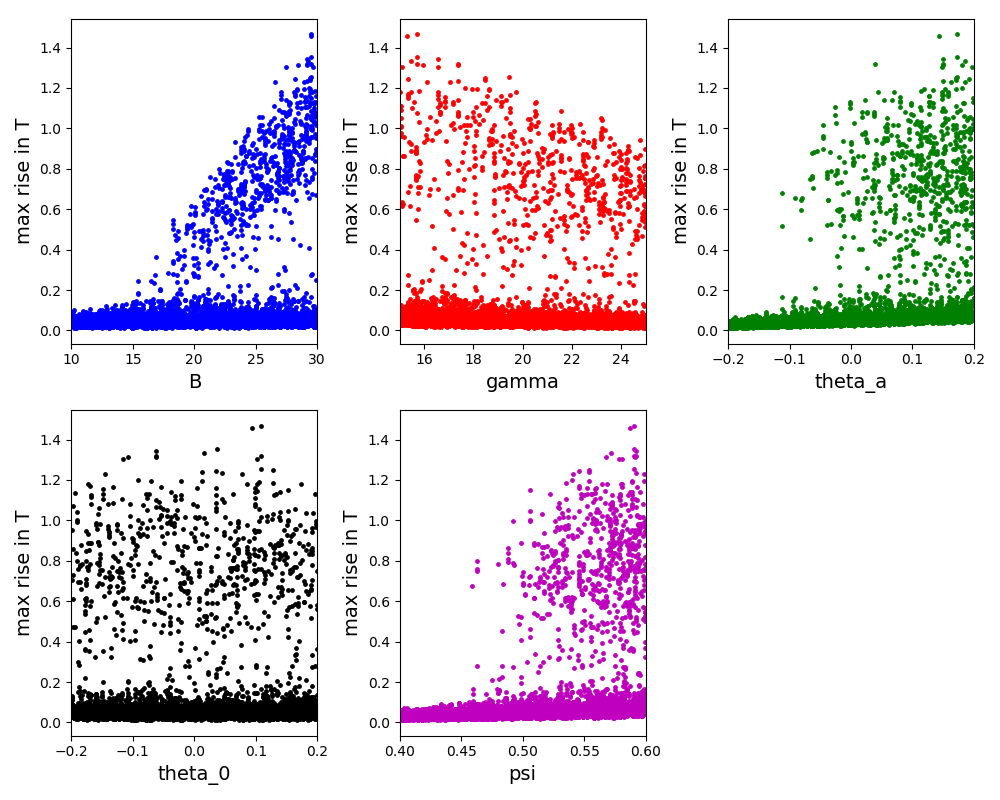
The scatter plot for the FAST method:

Files